通过前两周的《本地化适应是怎么发生的?》和《突变是否影响个体的适应性?》了解了群体的核酸多样性后,我们接下来就开始要着手进行功能基因的定位了。工欲善其事,必先利其器。在我们可以自由选用各类实验设计前,我们需要了解各种方法的基本原理。让我们先从连锁分析开始。
1. 连锁分析的基本原理
既然群体中产生了多样性,我们就期望将与性状相关的基因定位出来。在之前的文章中,我们提到功能基因定位的方法主要包括QTL定位(包含GWAS)和群体遗传(选择压力分析)。这里的QTL定位是广义上的QTL定位,包括经典的连锁分析和关联分析。在这里,我们先介绍一下连锁定位的方法原理。
连锁分析,之所以被称为“连锁分析”,其本质还是利用功能基因与分子标记间的连锁与重组,实现对功能基因位置的定位。
例如下图中,Q基因型会导致个体变高,q基因型会导致个体变矮。我们可以看到,邻近的基因座Bb与Qq基因座连锁。B总是与Q连锁,导致B基因型的个体总是更高,对应b基因型的个体更矮。而远离Qq基因座的Ee基因座则没有这种现象。由于两者距离较远,彼此间没有必然的连锁关系(倾向自由重组),因此我们可以看到E基因座对应的既有高的个体,也有矮的个体。
在实际研究中,这些分子标记ABCDE都是位置已知的标记,但我们不知道Qq基因座的位置。如果通过数学的方法,我们发现Bb、Cc基因座与性状高矮相关,而其他基因座并非如此,我们就可以确定功能基因Qq就位于Bb和Cc之间。
要创造这样的1个基因型分离的人工群体,我们往往需要使用杂交的策略(两种不同的亲本杂交),在之前小师妹的微信文章《遗传图谱各种作图群体介绍》曾经介绍过各类作图群体的来源方式,感兴趣的读者可以再看看。
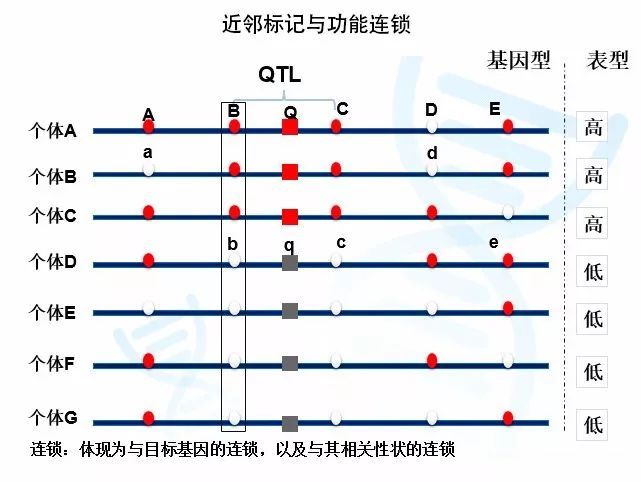
图1与功能基因的连锁与自由组合
2. 最简单的连锁分析方法
正如上文所说的,我们需要挖掘确认哪些分子标记与性状关联,从而进一步推断影响性状的功能基因与这类分子标记连锁,从而判断功能基因位于该分子标记附近。在统计学上,我们使用最简单的方差分析,也可以实现这样的推断。
如图2,我们可以将整个群体按照Bb基因座的基因型分为BB基因型群体和bb基因型群体的两个子群体。如果我们使用方差分析证明子群体BB的平均身高显著大于bb,则证明Bb基因座与性状相关。类似,我们将会发现按照Ee基因座分类的两个子群体在平均身高上则没有区别。这样我们就可以推断,由于Bb基因座与性状相关,那么决定身高的基因座Qq应该位于Bb附近,这样就实现了QTL初步定位。
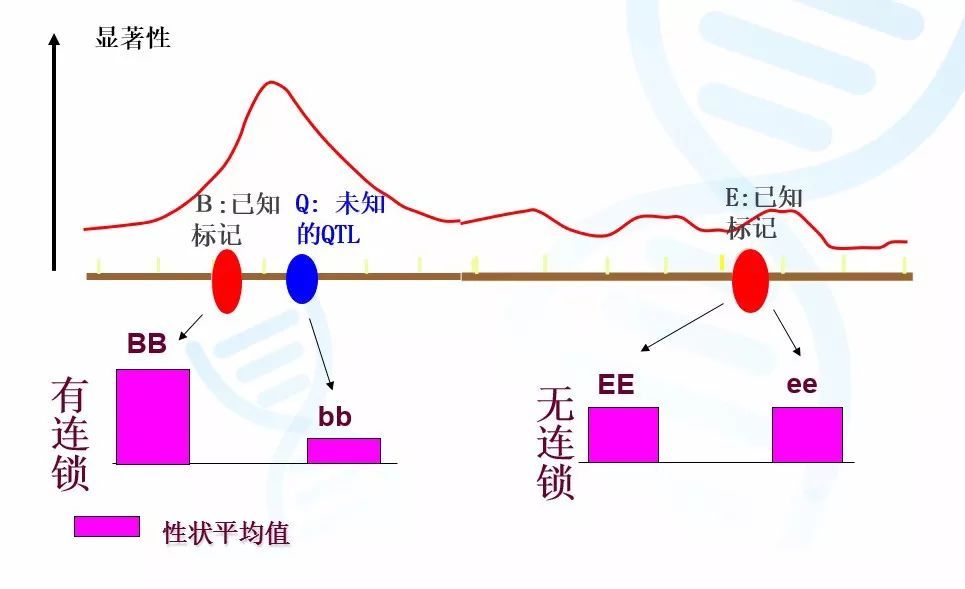
图2 使用方差分析进行单标记分析
3. 略复杂一点的连锁分析方法
再看看图1的示意图,我们是否可以将其看成1个线性回归方程组:
身高 = u+A*GT_A+B*GT_B+C*GT_C+D*GT_D+ E*GT_E
#方程1
其中u为群体均值(也就是方程的截距),系数A是A基因座的遗传效应,GT_A是Aa基因座的基因型,可能是aa、Aa、AA,当然数学上可以使用0,1,2替代。其中,系数A、B、C、D、E都是待求解的变量。
如果求解这个多元线性方程组,我们将发现A、D、E均为0(效应为0),而B、C则显著大于0,则一样推断Bb和Cc基因座对身高是有贡献的。那么,它们为什么对身高有贡献呢?因为它们与功能基因连锁啊,由此我们知道了功能基因的初步位置。这就是QTL定位中的线性回归模型。
4. 实际使用的简单的线性回归模型
以上的方程组在实际情况中,将可能会面临自变量的数量(标记数量)大于因变量(样本数),那么这个方程是不可准确求得唯一解的。所以,通常会将多元线性回归方程简化为一元线性回归方程组。例如,针对Aa基因座,我们可以构建一个方程组如下:
身高 = u+A*GT_A+e # 方程2
其中,e是随机误差效应。那么在这里的案例中,方程1就可以拆解为针对5个不同分子标记的方程2,从而一一求解每个标记/区间的效应。因为,这只是个简单的一元线性回归方程,求解起来是非常简单快速的。
这就是在连锁分析中常用的区间作图定位法(interval Mapping)的基本原理。
5. 实际应用最广的线性回归模型
实际应用最广的线性回归模型为复合区间作图定位(Composite interval Mapping)。单标记分析虽然效率很高,但却可能会带来误差,例如遗传背景的不均一给目标位点效应判断带来误差。
例如下图,个体A和B有三个QTL位点的差异。假设红色的基因型相比褐色的基因型可以将个体的高度提高10厘米。现在我想计算标记Marker1的效应,如果我们只考虑单一标记Marker1的效应(使用方程2),最终我们计算的结果以为A个体 30厘米的身高优势都来自Marker1的差异,就误把Marker1的效应计为30厘米(高估)。
但如果我们使用多元线性回归分析,将Marker2和Marker3并入方程组,在方程组中统一考虑它们的效应,那么对Marker1效应的估算将会更加准确(三个标记效应都是10厘米)。
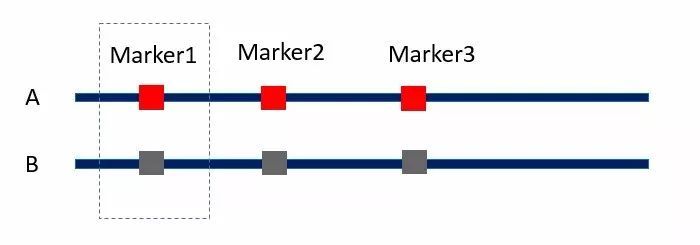
图3 目标QTL与背景QTL
在实际情况下,那些被忽略的背景标记效应会对单标记分析模型带来各种假阳性和假阴性的情况,所以背景标记的效应是必须被考虑的。
但目前的高密度遗传图谱,标记数量成百上千个,如上文提到的,如果每个标记效应都被并入方程,那么使用标准的方法这个方程组是无法求解的(方程1)。所以,在经典的复合区间作图定位中,采用了一个折中的方式,大体步骤如下:
a)使用单标记回归以及逐步回归的方法,从整个基因组中筛选若干个(例如10个)效应最强的标记。
b)在计算某个标记(区间)效应的时候,将其他区域效应最强的那些标记整合入方程组中,如以下方程式:
身高 = u+A*GT_A+[ B*GT_B+… …+ K*GT_K]+ e
# 方程3
在方差3中,未知变量一共有11个(A~K标记的效应),只要个体足够多这个方程还是可以求解的。其中目标标记是A(我们期望算出它们的效应)。B~K就是基因组其他区域的效应最强的标记,虽然我们暂时并不关心它们具体的效应,但将它们引入方程会让我们对A的效应估算更准。我们将B~K标记这种并非我们直接关心,但和自变量(A 标记)一样,同样对因变量(身高)有影响的标记称为协变量(covariant)。
所以,目前某些同行公司使用区间作图模型进行连锁分析,实际上是不对的。对于数量性状,只有使用考虑协变量的模型(例如复合区间作图)才是合理的方法。
6. 一些其他重要的概念
LOD值:这个p value的概念略有不同。P value是这个位点不存在QTL的概率。而LOD=log10(L1/L0),其中L1是这个位点有QTL的概率,L0是这个位点无QTL的概率。如果LOD=3,则意味着这个位点有QLT的概率是无QTL的概率的1000倍。
2-LOD置信区间:QTL定位的结果是1个LOD值在染色体上变化的波形图(如下图),QTL区域的LOD值会形成一个信号峰。功能基因理论上就位于信号最强(LOD值最大)的峰尖附近。但功能基因通常只是位于这个区间内,而不是必然位于峰尖。离峰尖距离越远的位置,LOD值不断下降,功能基因位于该位置的概率越低。
为了便于后续研究中筛选候选基因,我们通常会设置一个范围筛选候选基因。一般经验值会使用2-LOD置信区间。这个名词的意思就是LOD波动曲线从峰的最大值降低2的时候(Y轴),对应在遗传图谱上跨越的区域(X轴)。2-LOD置信区间大概对应99.8%的置信区间,即功能基因有99.8%概率已经落在这个区域内了。
1-LOD置信区间也是类似的概念,对应的置信区间大概是97%。
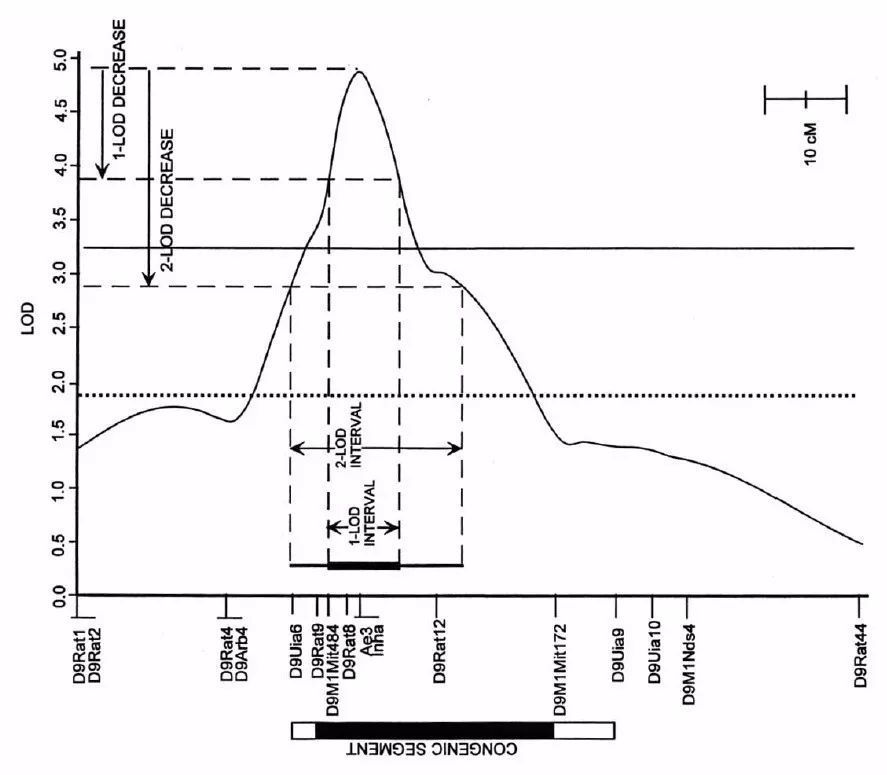
图4 QTL定位结果示意图
以上只是我们对QTL定位数学原理的科普性介绍,我们实际上略微简化了QTL定位中的模型以便利于初学者理解。要了解更多更专业的介绍,点击“阅读原文”可从Omicshare论坛相应的主题帖下载专业附件进行深入阅读。今天的内容就到这里啦~
- 本文固定链接: https://oversea.maimengkong.com/kyjc/829.html
- 转载请注明: : 萌小白 2022年1月16日 于 卖萌控的博客 发表
- 百度已收录
