PCA全名principal component analysis,即主成分分析,看到这个名字的时候,第一次深刻的体会到了什么是每个字都认识,合在一起却不知道是什么意思……
看一下主流的解释:主成分分析是一组变量通过正交变换转变成另一组变量的分析方法,来实现数据降维的目的。转换后得到的这一组变量,即是我们所说的主成分。
Emmmm,还是不懂……
拆开了,一个字一个词的来看:主成分分析的字面意思就是用主成分来分析数据呗!
首先,什么是主成分?
举两个简单的例子:
①评价一个研究生的综合能力有哪些指标呢:绩点、考研分数、科研能力、笔试成绩、面试表现、英语水平、奖学金等等等等……
②评价一座城市的发展水平有哪些指标呢:人口、GDP、面积、人均寿命、人均工资、人均受教育年份、性别比例、宗教人口、汽车保有量、人均住房面积等等等等……
一个指标就是一个变量一个维度啊,把他们画在图上直观的表示一下吧……
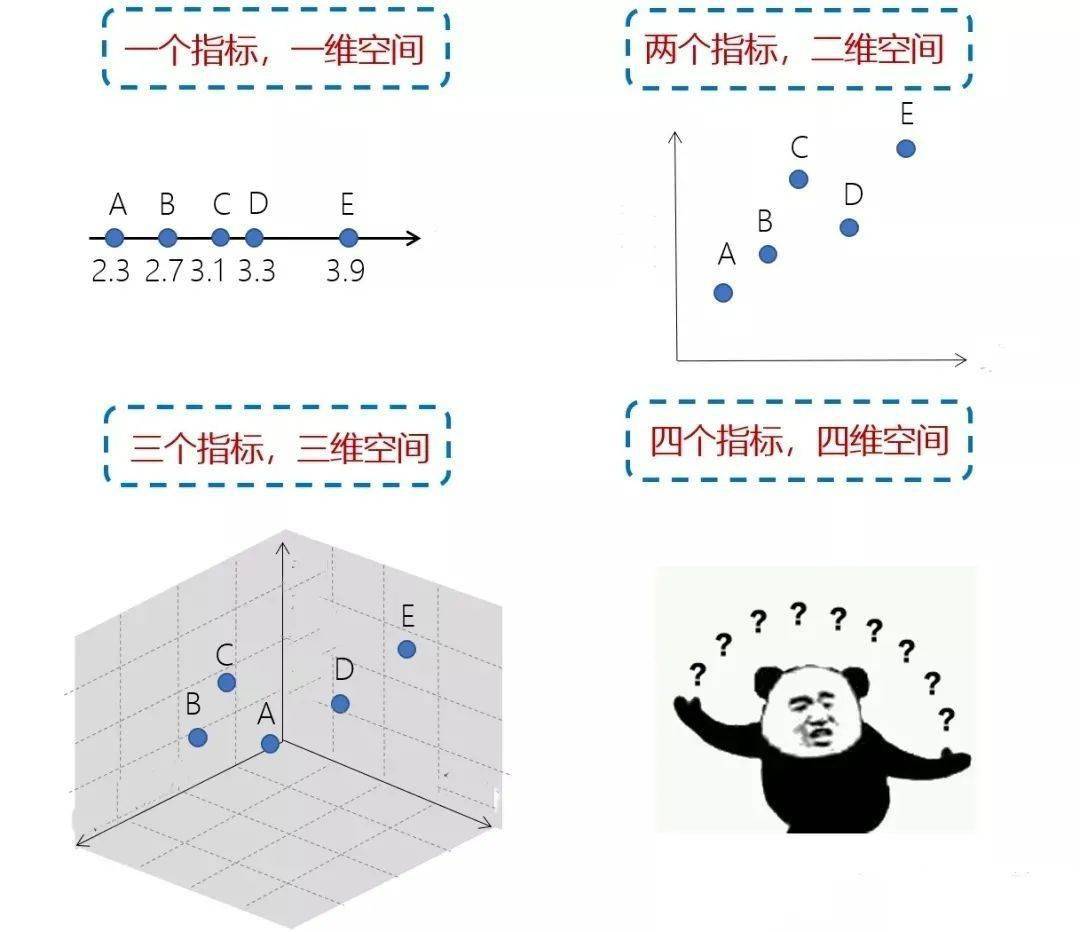
好家伙,超过三个我就画不出来了,那些基因、蛋白成千上万的,咋办?怎样用简单的方法来表示复杂的数据呢?
降维!
降维是通过减少数据中的指标(或变量)以化简数据的过程。这里的减少指标,并不是随意加减,而是用复杂的数理知识,得到几个“综合指标”来代表整个数据。而这里的综合指标就是所谓的主成分!它不是原来的指标中的任何一个,而是由所有原有指标数据线性组合而来。
为什么主成分可以代表这些指标呢?其实我们仔细看一下,这里的许多指标是有相关性的,比如绩点与奖学金、考研分数等有关联性,通过降维就可以帮助我们去除这些指标中重叠、多余的信息,把数据最本质和关键的信息提取出来。
那么我们就可以表示为:
将n个指标降维成r个主成分(r<n)后,这些个主成分会依据方差的大小进行排序,称作主成分(PC)1、主成分2、……主成分r。而每个主成分的方差在这一组变量中的总方差中所占的比例,即是主成分的贡献度。通常来说,我们仅考察贡献度前2或者前3的主成分,经过可视化后,即得到了二维或三维PCA散点图。
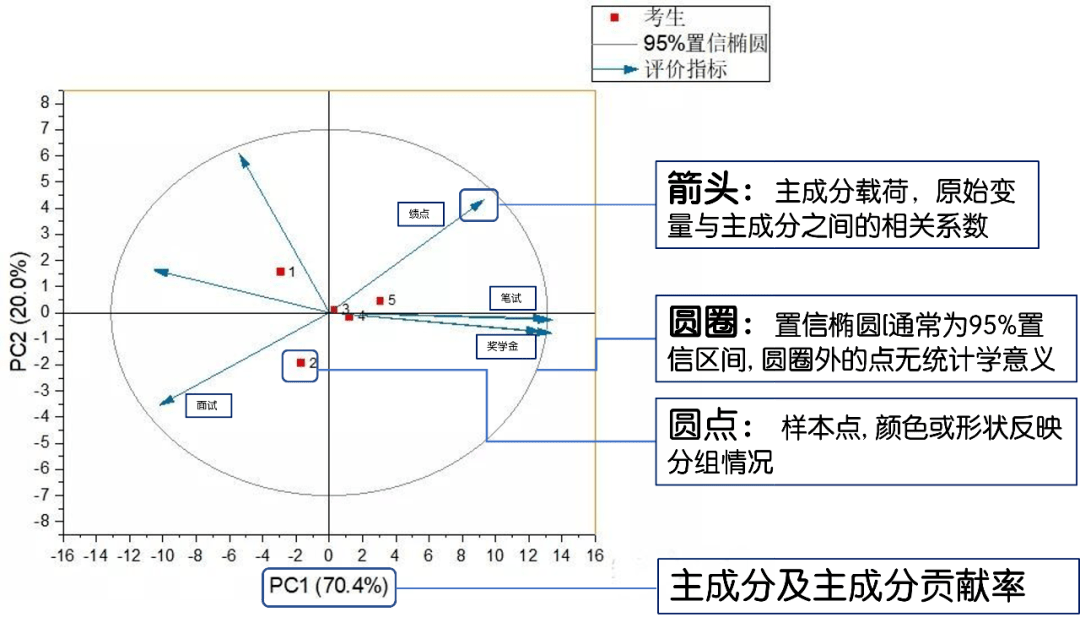
通过这样的可视化处理之后,可以帮助我们对数据做出清晰的了解:
1、各样本点连线的距离:体现每个学生之间的相似性,距离越短,相似性越大。
2、主成分与原变量之间的关系:箭头对应的原始变量在投影到水平和垂直方向上后的值,可以分别体现该变量与PC1和PC2的相关性(正负相关性及其大小)(例如,绩点对PC1具有较大的贡献,而面试则与PC1之间呈较大的负相关性)。
3、样本点和箭头之间的距离:反映样本与原始变量的关系。(对于3号样本点而言,各个指标都趋近于0,即各个指标都不是那么优秀)。
这样看下来,3、4号学生较为相似,1号2号5号有各自突出的特点。
所以,看PCA图抓住一点:样本点连线距离长=样本之间差异性大,样本点连线距离短=样本之间差异性小。这样可以让我们非常直观地看出各个样本之间的相似性。
例如在一张PCA散点图中,数个样本的点聚在一起,那么就说明这几个样本之间的相似性非常高;反之,如果几个样本的点非常分散,则说明这几个样本之间的相似性比较低。例如下图,几个组的样本对应的散点在组内呈现相互聚集的情况,说明组内的重复性比较好,样本数据非常相似,而组间则有较好的区分度。有的时候为了说明组内样本的相似程度,还会用一个椭圆将同一组的样本对应的散点全部囊括起来。
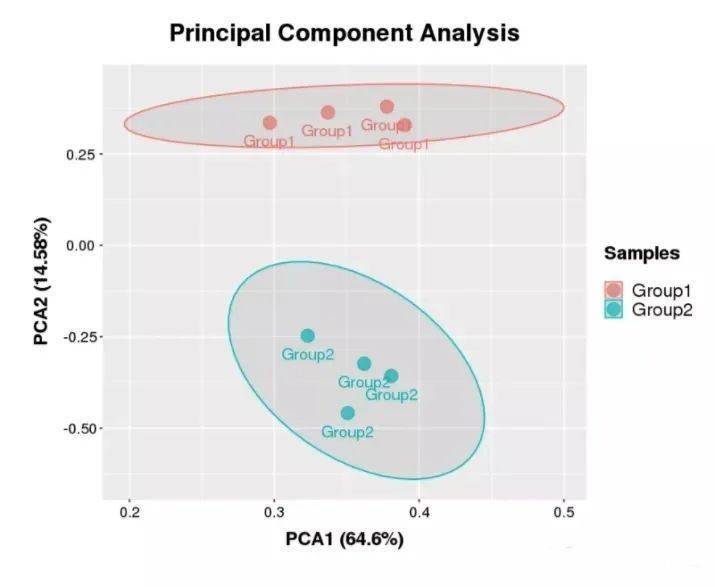
所以,通过PCA后,我们既可以直观的了解到到每个样本的特征,又可以将样本进行聚类,看他们之间的相关性和差异性。
在医学领域中,我们可以用PCA图来进行疾病危险因素分析,肠道菌群聚类分析,推断肿瘤亚群之间的进化关系......还用它来观察样本的分组、趋势、剔除异常数据,在文献中出现率还是很高的!
2.https://blog.csdn.net/weixin_39532754/article/details/110160445- 本文固定链接: https://oversea.maimengkong.com/image/990.html
- 转载请注明: : 萌小白 2022年6月16日 于 卖萌控的博客 发表
- 百度已收录
